Гормони щастя

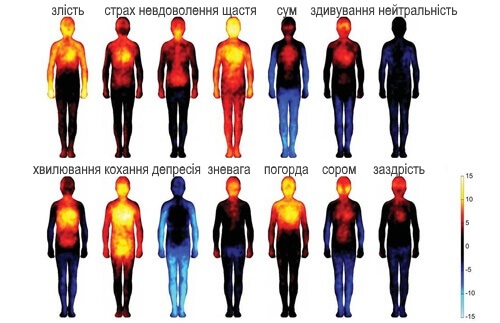
Як працюють «гормони щастя»

Всі ми чули вислів «гормони щастя». Невже омріяне щастя — результат хімічних процесів? Ми вирішили з’ясувати, що це за гормони, і як вони працюють.

Гормони щастя — що це?

«Гормонами щастя» прийнято називати серотонін, ендорфін і дофамін. Серотонін виробляється в шишкоподібної залозі головного мозку. Як хімічна сполука, серотонін відноситься до того ж ряду алкалоїдів індолу, що і психоделічні наркотики начебто ЛСД-25, псилоцибіна, ДМТ і буфотенина.

Він був відкритий в 1935 році італійським фармакологом Вітторіо Ерспамером, який назвав це речовиною, що скорочує гладку мускулатуру, ентерамином.

Через 13 років у клініці Влівленда Моріс Раппорт з колегами виявив судинозвужувальну речовину в сироватці крові, яка було названа серотоніном. В 1952 році було доведено, що серотонін і ентерамин — це одна і та ж речовина, а ще через рік серотонін був виявлений в головному мозку.

Ендорфіни представляють із себе групу хімічних сполук, за способом дії схожих з опіатами. Вони утворюються виробляється гіпофізом речовини беталіпотрофіну. Серотонін утворюється з амінокислоти триптофану.

Нейромедіатр дофамін виробляється в головному мозку і наднирниках. Він відіграє велику роль в «системі винагороди» мозку і виробляється під час позитивного для людини досвіду.

Чи дійсно серотонін робить людину щасливою?

З серотоніном все не так просто. Уявлення про матерію як про панацею від смутку і депресії невірно. В даний час вплив серотоніну на поведінку людини ще недостатньо вивчено. Він впливає по-різному на різні ділянки мозку, і цей вплив нерівномірно і залежить від взаємодій з іншими гормонами.

Найменша концентрація серотоніну в корі та мозку, найбільша – активує ретикулярну систему, де він грає важливу роль в циклі сну-неспання. Коли рівень серотоніну тут підвищується, мозок занурюється в глибокий сон.

Дослідження, що проводилися в психіатричних клініках, показали, що надмірний вміст серотоніну виявляється в мозку душевнохворих.

Сьогодні вже доведено зв’язок між дефіцитом серотоніну і агресією. Це пов’язаність язано з тим, що серотонін контролює інші трансмітери і «вирішує», пропускати той чи інший сигнал у мозок. Коли серотоніну недостатньо, цей контроль слабшає і адреналінові реакції включають в мозку механізми паніки, агресивності навіть тоді, коли видимих причин для цього немає.

Профіцит серотоніну також може негативно позначитися на здоров ї та поведінці людини. Так, підвищений вміст серотоніну спостерігається при аутичних станах. Нездатність рецепторів зв’язку зв’язати велику кількість серотоніну також зазначалося у людей, страждаючих хворобою Альцгеймера.

Щасливі гени

Останні дослідження довели, що для належного рівня щастя людині потрібні відповідні гени, а точніше, так званий ген 5-HTTLPR, який відповідає за транспортування вже згадуваного серотоніну. Для того, щоб це довести, вчені Лондонської медичної школи та школи економіки опитали кілька тисяч чоловік. Результати підтвердили припущення: волонтери, у яких було дві копії гена щастя від обох батьків, виявилися оптимістами, не схильними до депресії. Результати дослідження були опубліковані Ян-Еммануелем де Неві в журналі Journal of Human Genetics.

Вчений також підкреслив, що незабаром можуть бути знайдені й інші «щасливі гени». Однак Ян-Еммануель не стверджує, що при несприятливих умовах люди з «щасливими генами» не зазнають депресії. Гени генами, але реакції організму на негативні фактори ніхто не відміняв.

Щаслива страва

Як ми вже знаємо, серотонін утворюється з амінокислоти триптофану. Потреба в ній може задовольнятися лише вступом її з-зовні, тому життєво важливо споживати «правильні» продукти, що сприяють виробленню серотоніну і ендорфінів. Триптофан — компонент харчових білків, що містяться в соєвих бобах, банани, фініки, горіхи, гриби, вівсі.

Благотворно на вироблення серотоніну також позначається споживання шоколаду, картоплі, авокадо, кінзи і іншої зелені, молока, цитрусових, цільнозернового хліба і сиру. Рівень ендорфінів також підвищується при прослуховуванні музики та від занять сексом.

Важливо пам ” ятати про те, що триптофан перетворюється в серотонін в шишкоподібної залозі тільки при сонячному світлі, тому не потрібно нехтувати прогулянками та відпочинком на свіжому повітрі. Зимова сезонна депресія — із-за нестачі природного світла. Також виробленню ендорфінів сприяють заняття спортом. Людина може в прямому сенсі, «добігти до щастя».

Що шкодить гормону щастя?

Негативно позначається на вироблення «гормонів щастя» прийом будь-яких наркотичних речовин. Із-за їх вживання порушуються медіаторні мозкові зв’язки. По суті, синтетичні психоактивні речовини обманюють мозок, видаючи себе за серотонін. Швидкий викид ендорфінів у плазму крові і мозок після вживання стимуляторів провокує звикання до цього рівня. Згодом організм перестає виробляти необхідні гормони, що вкрай негативно позначається на хімічному балансі організму, призводить до депресії та інших негативних наслідків

Як негативні емоції шкодять організму

Чи знаєтет ви, що емоції впливають на наше здоров'я. Давайте розглянемо, як негативні емоції шкодять організму.

Чи замислювалися ви над тим, як спосіб вашого мислення та емоції можуть впливати на здоров’я та організм? Ми часто навіть не уявляємо собі на скільки такий вплив може бути серйозним. Ми іноді дозволяємо стресовим ситуаціям, напрузі, тривозі, депресії, метушні та іншим негативним почуттям заволодіти нами. В цей момент ми не враховуємо, що це може вплинути на наше фізичне та психічне здоров’я, знижуючи якість життя.

Поєднання душі та тіла – це набагато сильніший зв’язок, ніж ми думаємо. Наші думки та емоції стимулюють виділення певних хімічних речовин, які впливають на наше фізичне та емоційне здоров’я.

Наприклад, серотонін і дофамін – дві хімічні речовини, які виробляються нашим мозком, коли ми відчуваємо щастя або ейфорію. Аналогічний процес відбувається з негативними емоціями. Замість того, щоб впливати на організм добре, вони викликають біль та певні хвороби, які заважають нам відчувати радість життя.

Мозок має здатність зберігати важливу та вирішальну інформацію, що стосується нашої поведінки та ставлення до певних ситуацій. Багато експертів сходяться на думці, що ми всі здатні та маємо можливість бачити дві сторони в кожній ситуації: хорошу та погану. Саме через це ми несемо відповідальність за те, якого значення – позитивного чи негативного – ми надаємо таким моментам, і за те, як ми сприймаємо такі ситуації.

Як емоції впливають на організм

Наші емоційні стани можуть призвести до фізичних недуг. А фізичний стан, в свою чергу, може нам підказати, що ми переживаємо важкий час, в якому негативні думки та емоції взяли контроль.

Наприклад:

Хронічний біль шиї може вказувати, що, можливо, нам слід звернути увагу на наші емоції або навіть спробувати переоцінити певні обставини, які ми досі сприймали лише з негативної сторони.
Незрозумілий біль у стегнах може бути знаком того, що нами заволодів певний страх, а ми не в змозі приймати важливі рішення.
Біль у верхній частині спини може бути пов’язаний з якимось горем.
Біль у середній частині спини пов’язаний з неможливістю відпустити, забути минуле.
Біль в попереку пов’язаний з переживаннями щодо фінансових негараздів.
Больові відчуття у колінах можуть вказувати на страх, гордовитість та відсутність контролю над егоїзмом.

Коли ми переживаємо ситуацію, яка змушує нас сердитися, в організмі відбувається біохімічна реакція. Вона підвищує рівень адреналіну, що, в свою чергу, змушує нас переживати стресову ситуацію, яка це спричинила, знову і знову.

Почуття засмучення можуть значно впливати на нашу енергійність та мотивацію. Печаль викликає виснаження, значну втому та низький рівень сили волі.

Як боротися з виникненням негативних думок і почуттів?

Зрозуміло, що у кожного в житті є велика кількість моментів повних щастя, проте саме важкі часи перевіряють нашу здатність контролювати свої емоції. Щоб впоратися з негативними думками і почуттями, важливо навчитися мислити позитивно, незалежно від того, наскільки важкими чи непереборними події можуть здаватися.

Кожного дня, коли ми прокидаємося, важливо підготувати тіло та розум до нового дня та викликів, які він нам приносить. Це потрібно для того щоб ми могли залишитися здоровими та щасливо жити.

Додайте трохи позитиву

Наш розум на диво потужний та може легко впоратися з безліччю завдань одночасно. Отже, дуже важливо забезпечити його хорошою дозою позитиву та спробувати побачити світлу сторону речей. Навіть якщо ви знаєте, що перед вами стоїть завдання подолати відносно важку ситуацію.

Коли негативні думки та емоції переважають у нашому житті, це безумовно вплине на здоров’я. Отже дуже важливо знайти кілька хвилин, щоб задуматися, обміркувати чи справа насправді варта потраченого часу і енергії, а тим більше негативних емоцій.

Швидше за все, що після таких роздумів, замість скаржитися на долю та дозволити своїм емоціям керувати вами, ви захочете внести зміни у вашу поведінку. Почнете шукати таке вирішення проблеми, щоб її негатив не знизив якості вашого життя.

Науково доведено, що позитив і хороші емоції, такі як радість і щастя, вивільняють гормони, відповідальні за посилення імунної системи. Крім того, було встановлено, що негативні емоції мають протилежний ефект і послаблюють імунну систему. Вони роблять наш організм більш схильним до різних хвороб.

Отож, маймо на увазі, хороші думки та емоції, позитивне мислення та сприйняття проблем з оптимізмом є питанням вибору кожної людини. Хороша доза позитиву вартує зусиль, оскільки саме позитив покращує наше фізичне та емоційне здоров’я у багатьох аспектах.

Всі ми знаємо, що таке страх, біль, багато хто знає що таке закоханість або відчуття щастя. Однак з наукової точки зору всі ці емоції - не більше ніж реакція на певні хімічні речовини, які синтезуються в нашому організмі. Нижче наведені хімічні формули цих речовин у максимально спрощеному і популяризованому вигляді.